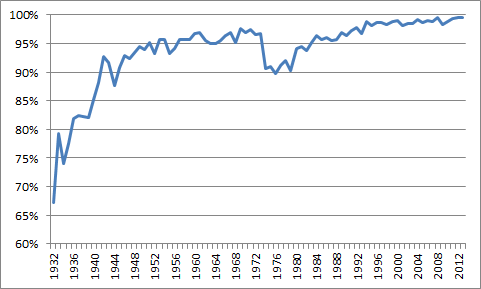
 The NFL’s Competition Committee is currently considering rules changes to eliminate the boredom associated with the extra point. As you can see from the graph above, extra points are practically automatic now, to the tune of a 99.6% conversion rate in 2013. In fact, extra points have been close to automatic for awhile; the success rate was even as high as 96.8% in 1973, the last year the goal posts were still right on the goal line. The conversion rate was depressed for about 15 years before bouncing back to 97% in 1989, and there have been just 18 missed extra points total in the last three years. I don’t disagree that something could be done to improve the quality of the game.
The NFL’s Competition Committee is currently considering rules changes to eliminate the boredom associated with the extra point. As you can see from the graph above, extra points are practically automatic now, to the tune of a 99.6% conversion rate in 2013. In fact, extra points have been close to automatic for awhile; the success rate was even as high as 96.8% in 1973, the last year the goal posts were still right on the goal line. The conversion rate was depressed for about 15 years before bouncing back to 97% in 1989, and there have been just 18 missed extra points total in the last three years. I don’t disagree that something could be done to improve the quality of the game.
The simplest alternative is to make touchdowns worth seven points instead of six, and to allow a team to gamble one of those points in the hopes of getting two points by “going for two.” In other words, we would have the system we have now, except that the song and dance of actually kicking the extra point is replaced with an automatic point.
Another solution is to eliminate the extra point entirely, requiring that teams go for two after every touchdown. I won’t try to answer the subjective question of whether or not this would make for a more enjoyable fan experience; the more interesting question to me is whether or not this would lead to more upsets. In other words, if teams had to go for two after every touchdown, would this lead to the better team winning more or less often? I posed this question on the Footballguys.com message boards and got into a good discussion there, much of which I’ll summarize here.
Before analyzing, we must recognize that the two-point play is not like a typical NFL play. A team that’s great in short yardage (say, Carolina) would probably be better off than most teams at converting on these attempts. Likewise, teams that excel in goal-line defense but maybe don’t have great corners (like say, Carolina) would probably be better off, too. But I think, on average, good teams are better at converting two point plays than bad teams, and, on average, good teams are better at preventing two point conversions than bad teams.
So how would such a rule change impact NFL games? One argument that this rule change would make the better team more likely to win is that this would present an additional hurdle for the weaker team. By replacing a play where everyone is successful with a competitive play, this increases the sample size, generally a bad thing for underdogs. Right now, a weaker team only needs to match the stronger team touchdown for touchdown (and field goal for field goal and safety for safety). But if the weaker team matches the better team under this new regime, the weaker team, on average, will still be trailing. By increasing the sample size of relevant plays, the weaker team needs to outplay the better team for longer, making it harder to pull the upset.
On the other hand, the argument is probably more convincing the other way that a mandatory “go for two” rule would lead to more upsets. That’s because the 2-point conversion play is a high-leverage play, and the inclusion of more high-leverage plays is generally a positive circumstance for the underdog. Imagine a rule change where the NFL made going for 2 mandatory, but made the successful outcome worth 20 points. That environment would almost certainly make things better for weaker teams: instead of having to outplay the better team for 60 minutes, the weaker team could be outplayed and win as long as they won on two or three key plays. That’s taking the example to its extreme, but one could argue that the same idea holds with the conversion worth two points, even if the effect would obviously be muted.
Here’s another way to think about it. Let’s ignore games that aren’t very competitive, because the outcomes of those games won’t change under the current format or the “mandatory go for two” environment. But there are three other types of games:
1) Close games where the better team narrowly wins
Suppose the better team scores three touchdowns and a field goal, and the worse team scores three touchdowns. Under the current system, the weaker team has no chance to win. Under the new system, it’s at least possible that the weaker team can win (by winning on at least 5 out of the 6 two-point conversion attempts in the game).
Or a game where the better team scores a touchdown and the weaker team scores two field goals. The score could be 21-20 or 28-27 or 7-6, but now, a touchdown always beats two field goals. In the mandatory go-for-two environment, the weaker team can win by stopping the better team on their 2-point attempts. Since “close games where the better team narrowly wins” is presumably the most likely of these three events to occur, a rule change that requires teams to go for two should make things slightly better for the underdog.
2) Games that go to overtime
In overtime, the weaker team has something very close to a 50/50 chance of winning. In say, a 24-24 game under the old environment, there would be six two point conversion attempts. If the better team wins on at least 4 of them — and we assume, on average, that the better team would be better in this situation — then they win in regulation. So we might say that the “mandatory go for two” rule hurts the weaker team, although it’s a debatable point (one could argue that the odds of the weaker team winning in overtime are say, only 40 or 45%, and there’s at least that good of a chance if not greater that the weaker team wins on at least 3 of the 6 two-point plays).
Here’s yet another way to think about it. Right now, a 21-21 game is an overtime game. Would the better team prefer to play an overtime period, or prefer to run six two-point conversion plays, 3 on offense and 3 on defense, to declare the winner? That question doesn’t have an intuitive answer for me.
3) Games that the weaker team narrowly wins
Obviously the weaker team prefers the old environment here. The 24-21 game could be flipped to a 22-21 game if the weaker team goes 0/3 on two-point attempts and the better team goes 2/3. Now scenario 3, by definition, should happen less than scenario 1, but we have to consider this when analyzing the question overall.
In other words, Scenario 3 won’t happen as often as Scenario 1, but Scenario 3 is more likely than Scenario 1 to be flipped. Which effect is larger? I’m open to debate, although I think the “mandatory go for two” rule would result in slightly more upsets. While it’s a complicated (and in my opinion, a very interesting!) question to analyze, I think I fall on the side that adding more high-leverage plays tends to result in more upsets. Whether or not that’s a good thing is up to you to decide.
