The New York Giants are now 0-6. There are many reasons for the team’s struggles: questionable drafting, injuries, Eli Manning interceptions, injuries, coaching mistakes by Tom Coughlin, and injuries. But let’s say you have a buddy who is convinced that the Giants are not that bad: in fact, he thinks New York is just a .500 team that has been really unlucky.

Your first inclination might be to stop being friends with this person, but after that, you might wonder: “Hey, how likely is it for a .500 team to start off 0-6?” This is the same (ignoring strength of schedule, the fact that games are not independent, and several other variables) as asking the question “how likely is a coin to land on heads six times in a row?” The answer to both questions is pretty simple: 0.500^6, or 1.56%. Using the binomial distribution (in Excel, this would involve typing =BINOM.DIST(0,6,0.5,TRUE) into a cell) — which assumes that the talent level of NFL teams is normally distributed, an assumption I will make throughout this post — would give you the same result of 1.56%.

That answer is simple, but it actually answers a different question. What you want to know is the likelihood that the Giants are actually a .500 or better team. It’s a minor but crucial distinction: what we just determined was the likelihood that, given the assumption that the Giants are a .500 team, that they would start 0-6. To address the question of how likely the 2013 Giants are actually a .500 (or better) team despite the 0-6 start, we need to use Bayes Theorem.

Much of the math involved in this process is frankly over my head, but fortunately, Kincaid over at 3-D baseball already did much of the work (and thanks to Neil for giving me that link). I will be blatantly copying his article (with the only changes being stylistic and making this for, you know, football), so make sure to give him all the credit he deserves. It’s a fantastic piece that has many useful applications.

What we want to find out is the probability of A (the Giants being a .500 or better team) given B (the Giants going 0-6).  This can be stated as:

P(A|B) = P(B|A)*P(A)/P(B)

To determine the probability of A given B (which is what P(A|B) means in English), we need to find the probability of B given A, multiply that by the probability A, and divide by the probability of B.

Let’s start with the probability of A, which is simply the odds that a random NFL team (in this case, the Giants) are a .500 or better team.  That’s easy: it’s 0.500. In this step, we’re not looking at the results: we just want to know how likely the team we pulled from our prior distribution is actually a .500 (or better) team.  In truth, I’m taking the easy way out here by picking .500; if we want answer the question of how likely a 9-7 team (the Giants record last year and their wins total according to Vegas in the pre-season) is to start 0-6, that’s a slightly more complicated question.  This post is complicated enough, so we’ll skip that part for now.  In conclusion, P(A)=.5.

The more interesting question is determining the probability of B, i.e., the probability that we observe a random team drawn from our prior distribution lose its first six games. This is simple to calculate for any one team if we know their true winning percentage — after all, we did that in the beginning of this post — but we need to know the average weighted probability for all possible teams we could draw from our prior distribution. We need an average weighted probability because if a team goes 0-6, they’re much more likely to be a bad team than a good team. Doing this will require a bit of calculus, but fortunately there are online calculators that can do all the heavy lifting.

For any one team with a known true win% (p), the probability of going 0-6 is:

( G! / (W! * L!) ) * p^W * (1-p)^L

where G represents the number of total games, W the number of wins, and L the number of losses. This isn’t as scary as it looks: if we make G = 6, W = 0, and L = 6, and want to see the likelihood of a team going 0-6 as p (the known true win%) ranges from 0.25 to 0.75, we get the following graph:

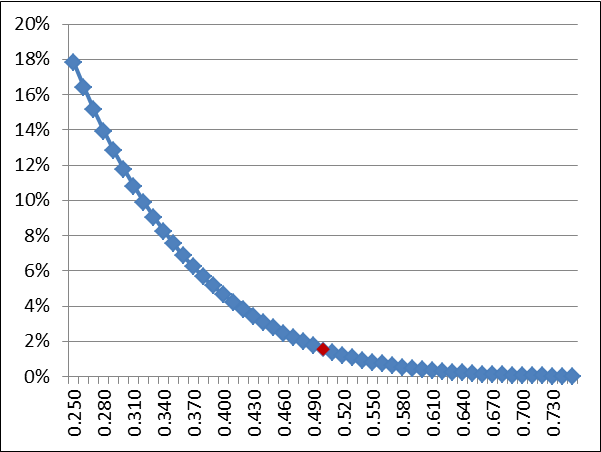
The red dot is at p = 0.500, which shows the Giants at a 1.56% chance.   But the key isn’t finding the odds of each p, it’s finding the average value of that formula across the entire prior distribution. To do this, we utilize the same principle as a weighted average. Here, the weight given to each possible value of p is represented by the probability density function of the prior distribution. As you can see above, the odds of a .300 team losing six straight games is much higher — about 11.8% — and that number gets weighted by the quantity f(p), where f(p) is the probability density function or our prior normal distribution. We repeat this for each possible value of p, add up the weighted terms, and then divide by the sum of the weights. This means taking the definite integral (from p=0 to p=1) of the probabilities weighted by f(p), which we can do using an online definite integral calculator. You can copy and paste this into the function field if you want to try it for yourself:

((6!/(0!*6!))*exp((-((x-.5)^2))/(2*.0225))*(x^0*(1-x)^6)/(sqrt(2*3.14159*.0225)))

or, more generally, if you want to play around with different records or different means and variances for the prior normal distribution:

(((W+L)!/(W!*L!))*exp((-((x-u)^2))/(2*VAR))*(x^W*(1-x)^L)/(sqrt(2*Pi*VAR)))

Note: this formula has one variable in there I haven’t discussed, which is the variance (represented by VAR in the equation). I used 0.0225 as the variance, and you can read why in this footnote. ((From 2002 to 2012, the standard deviation of team winning percentages was 0.192. However, there’s a lot of noise in team winning percentages. The standard deviation in Pythagorean winning percentages was 0.173 over that same time period. There’s still some noise in Pythagorean winning percentage, too. What we want to use here is the spread of true talent — not observed production — in the NFL, which is certainly smaller than 0.192 and I would presume to be a bit smaller than 0.173, too. I’ll use 0.15, which is a somewhat round number, to estimate what the true standard deviation is for NFL teams. The variance is simply the square of the standard deviation, which is why I used 0.0225. Note that Kincaid stated that for baseball, the true standard deviation was 0.05, a much lower number. That may be appropriate for football, too, but a full discussion is outside the scope of this post.)) Anyway, integrating the above equation from 0 to 1, we get a total value of .042. We still have to divide by the total sum of the weights to find the weighted average, but that is equal to one by definition (it is just F(p), or the cumulative distribution function of the prior distribution). Therefore, P(B) = .042.

Finally, we have to calculate P(B|A). This is the probability of observing an 0-6 record, given that we are drawing a random team from the prior distribution that fulfills condition A, which is that the team has at least a .500 true winning percentage. This is done very similarly to finding P(B) above, except we are only considering values of p > 0.500.

Start by calculating the same definite integral as before, but from .5 to 1 instead of from 0 to 1 (this is done by simply changing text box next to “Lower limit” below the formula). This gives a value of .00261. That is the weighted sum of all the probabilities; to turn the weighted sum into an average, we still have to divide by the sum of all the weights, which in this case is .5. Dividing .002612 by .5 gives us .005226. This is P(B|A).

Hey, we’re almost done! Now we have:

P(A)= .5 (this is the probability of randomly selecting a team that is average or better)
P(B) = .042 (this is the probability that we observe a random team drawn from our prior distribution lose its first six games)

P(B|A) = 0.005226 (the probability of B, given A)

P(A|B) = .005226 * .5 /.0420 = 6.2%

So the probability of a team that goes 0-6 being at least a .500 team in terms of true ability is about six percent (assuming our prior distribution is fairly accurate), although it may even be as high as 27.8 percent ((If you used a standard deviation for NFL team winning percentage of 0.05 instead of 0.15, that would be the result. In other words, the more tightly packed the teams are, the more likely it is that a good team is the one actually producing the 0-6 record)). Once again, kudos to the outstanding Kincaid for doing all the heavy and medium lifting, so even I could figure it out. And as he pointed out, one of the interesting results is that this result — 6.2% — is quite a bit larger than the 1.56% result you would get from simple math, which was essentially just a hypothesis test. In his words:

This is why it is important not to misconstrue the meaning of the hypothesis test. The hypothesis test only tells you a very specific thing, which is how likely or unlikely the observed result is if you assume the null hypothesis to be true. Rejecting the null hypothesis on this basis does not necessarily mean the null hypothesis is unlikely; that depends on the prior distribution of possible hypotheses that exist. Considering potential prior distributions allows us to make more relevant estimates and conclusions about the likelihood of the null hypothesis.

But we’re not done, so allow me to copy some more of his work. Another advantage of the Bayesian approach is that it gives us a full posterior distribution of possible results. For example, when we observe an 0-6 team, we can not only estimate the odds that it is a true .500 team, but also the odds that it is a true .550 team, or .600 team, or whatever. And since we have a full distribution of likelihoods, we can also figure out the expected value.

The posterior distribution of possible true talent W% for a team that is observed to go 2-10 is represented by the product we integrated earlier:

((6!/(0!*6!))*exp((-((x-.5)^2))/(2*.0225))*(x^0*(1-x)^6)/(sqrt(2*3.14159*.0225)))

We find the expected value of that function the same way we found the average value of the above probabilities. This time, we want to find the average value of x (or p, as we were calling it before), so we weight each value of x by the above function, and then divide by the sum of the weights. For the numerator, this means integrating the above function multiplied by x. To do that, just copy and paste this into the calculator:

x * ((6!/(0!*6!))*exp((-((x-.5)^2))/(2*.0225))*(x^0*(1-x)^6)/(sqrt(2*3.14159*.0225)))

The denominator is just the sum of the function not multiplied by x, which we already did above (i.e., 0.042).

Plugging this into the definite integral calculator, we get:

0.01279096/0.04203334 = 0.304

So a team that goes 0-6 games will be, on average, about a .304 team (again, assuming our prior distribution is accurate). That’s not far from the answer you would get if you added 5.5 wins and 5.5 losses to the Giants’ record, which is Neil’s preferred method of regressing teams to the mean. A team that was 5.5-11.5 would have a 0.324 winning percentage.

Some additional notes, which, like everything else in this post, comes courtesy of Kincaid. This analysis assumes a prior that presumes nothing about the team in question other than the fact that it comes from a distribution of teams roughly like that we observe in the NFL. What if, in addition to knowing the 0-6 team plays in the NFL, we also know that the team has Manning, Victor Cruz, Hakeem Nicks, Jason Pierre-Paul, and is expected to be one of the better teams in the league? We can adjust the prior for that information as well. Our prior distribution, after accounting for the amount of talent we believe to be on the team, might have a mean record of 9-7.

This would give us:

p(A) = 0.338 (in Excel, this is simply “=1-NORM.DIST(9/16,0.5,0.15,TRUE)” — this means only 33.8% of teams have true ability levels of 9-7 or better

p(B) = 0.023797

p(B|A) = 0.0024

Now we get an expected winning percentage for the rest of the season of .349; in other words, we would put a new over/under on number of wins for the Giants this year at 3.5 wins. Of course, this all depends on what prior you assume (and we’ve ignored injuries and strength of schedule), but as long as you make reasonable assumptions, this process should provide a reasonable estimate.